腾讯云优惠活动, 点击链接进行购买一年仅需99元

腾讯云限时开团活动, 点击链接进行购买一年仅需95元

# 教你实现微信 8.0『炸裂』的 🎉 表情特效

# 写在开头

最近微信更新了 8.0，其中之一最好玩的莫过于表情包的更新了，大家都在群里纷纷玩起了表情包大战。

作为一个前端程序员，这就勾起了我的好奇心，虽然我从来没有实现过这样的动画，但是我还是忍不住想要去实现，最终我花了 2 天时间去看一些库的源码到我自己实现一个类似的效果，在这里我总结一下，并且手把手地教大家怎么学习实现。而 🎉 有一个自己的名字，叫做五彩纸屑，英文名字叫 confetti。

聊天室+五彩纸屑特效在线地址: https://www.qiufengh.com/#/

聊天室 Github 地址: https://github.com/hua1995116/webchat

五彩纸屑 Github 地址: https://github.com/hua1995116/node-demo/tree/master/confetti

特效预览，时间原因我只实现了平行四边形的彩色小块，其他形状的原理也是类似。

还可以设置方向

# 前期研究

在写这个特效前，我几乎不会用 canvas，虽然说现在也不太会用，很多 API 也不太清楚，因此这篇教程也是基于零基础 canvas 写的，大家不用担心这个教程难度太高而被劝退。我会通过零基础 canvas 的基础上来一步步实现的。不过学习这个特效之前需要一点点高中数学的知识，如果你还记得 sin 和 cos 函数，那么以下的内容对于你来说都会非常简单，不会也没关系~

我个人比较喜欢探索研究，对有意思的玩意儿就会去研究，因此我也是站在巨人的基础上，去 codepen 查了好多个类似的实现进行研究。

最终将目标定位在了 canvas-confetti (opens new window) ，为什么是这个库呢？因为他的效果对于我们来说非常可以了，而且它是一个开源库，并且拥有了 1.3K star（感觉改天可以分析分析大佬实现库的原理了~），维护频率也非常高。

# 核心实现

# 切片场景

首先拿到这个库的时候，我有点开心，因为这个库只有一个单文件。

但是，当我打开这个文件的时候，发现不对...1 个文件500 行代码，我通过剥离层层的一些自定义配置化的代码，最后抽离出单个纸屑的运动轨迹。我就开始不断地在观察它的运动轨迹...无限循环的观察...

可以看到它在做一个类似于抛物线的运动，然后我一一将源码中的变量进行标注，再结合源码。

fetti.x += Math.cos(fetti.angle2D) * fetti.velocity;
fetti.y += Math.sin(fetti.angle2D) * fetti.velocity + fetti.gravity;

以上代码看不懂也没事，我只是证明一下源码中的写法，并且提供学习源码的一些思路，以下才是真正的开讲实现！

# 平行四边形的实现

实现这个特性前，我们需要知道 canvas 几个函数。更多查看（https://www.runoob.com/jsref/dom-obj-canvas.html）

beginPath

方法开始一条路径，或重置当前的路径。

moveTo

把路径移动到画布中的指定点，不创建线条。

lineTo

添加一个新点，然后在画布中创建从该点到最后指定点的线条。

closePath

创建从当前点回到起始点的路径。

fill

填充当前绘图（路径）。

fillStyle

设置或返回用于填充绘画的颜色、渐变或模式。

既然我们要实现五彩纸屑，那么我肯定得先实现一个纸屑，我们就来实现一个平行四边形的纸屑吧！

我们都知道在 css 中实现平行四边形就是一个 div，默认就是一个盒子，而在 canvas 中并没有那么方便，那么怎么实现一个平行四边形呢？

四个点，我们只需要知道四个点，就能确定一个平行四边形。而 canvas 中的坐标系和我们普通的写网页略有不同，它是从左上角作为起始点，但是并不影响。

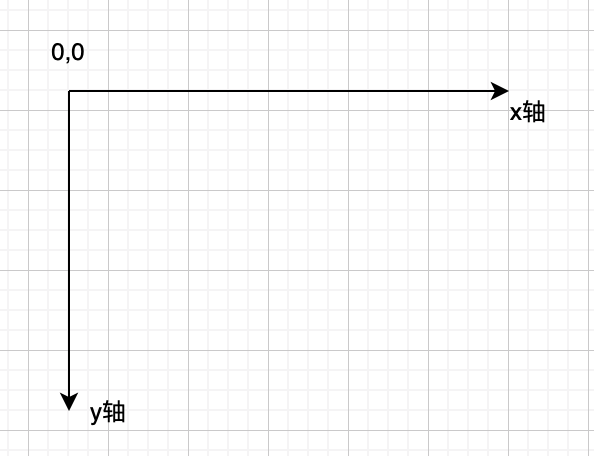
我可以来画一个宽为 20 的平行四边形，(0, 0), (0, 20), (20,20), (20,0)。

...(省略了一些前置初始化代码)
var context = canvas.getContext('2d');
// 清除画布
context.clearRect(0, 0, canvas.width, canvas.height);
// 设置颜色并开始绘制
context.fillStyle = 'rgba(2, 255, 255, 1)';
context.beginPath();
// 设置几个点
var point1 = { x: 0, y: 0 }
var point2 = { x: 0, y: 20 }
var point3 = { x: 20, y: 20 }
var point4 = { x: 20, y: 0 }
// 画4个点
context.moveTo(Math.floor(point1.x), Math.floor(point1.y));
context.lineTo(Math.floor(point2.x), Math.floor(point2.y));
context.lineTo(Math.floor(point3.x), Math.floor(point3.y));
context.lineTo(Math.floor(point4.x), Math.floor(point4.y));
// 完成路线，并填充
context.closePath();
context.fill();

我们总结一下，我们其实只需要一个点就能确定这个平行四边形的初始位置(0, 0)，如果再知道一个角度(90度)、以及平行四边形的变长(20)就能确定整个平行四边形的位置了！(仅仅只需要初中知识就能定位整个平行四边形)。

好了，你学会画这个已经离成功迈向了一大步！是不是挺简单的~

大佬们内心 OS: 就这？

嗯，就这。

# 运动轨迹

通过不断地调试 canvas-confetti (opens new window) 每一帧的轨迹运动，发现它始终做的是一个 x 轴变减速运动（直到速度为 0 就不继续运动了），而 y 轴也是一个先变减速运动再是一个均速运动，以下是大致的轨迹图。

这就是他的运动轨迹，别以为看着挺难的，但是核心代码只有三句。

// fetti.angle2D为一个角度（这个角度确定了运动轨迹 3 / 2 * Math.PI - 2 * Math.PI之间的一个值，由于要让轨迹往左上角移动，就是都要往负方向运动，因此选了以上范围），
// fetti.velocity 为一个初始为50长度的值。
// fetti.gravity = 3
fetti.x += Math.cos(fetti.angle2D) * fetti.velocity; // fetti.x 第一个点的x坐标
fetti.y += Math.sin(fetti.angle2D) * fetti.velocity + fetti.gravity; // fetti.y 第一个点的y坐标
fetti.velocity *= 0.8；

总结起来就是，第一个坐标点的 x 周始终在增加一个负值（Math.cos(3 / 2 _ Math.PI - 2 _ Math.PI) 始终为负值），这个值在不断减小。而第一个点的 y 轴也始终在加一个负值 Math.cos(3 / 2 _ Math.PI - 2 _ Math.PI) 始终为负值），但是由于 fetti.gravity始终为正值，因此到了某个临界点，y 的值会不断增加。

我模拟了以下的坐标，由于为了让大家能明白这个轨迹，以下坐标轴和 canvas 中相反，数据我也做了相应的处理，进行了反方向处理。

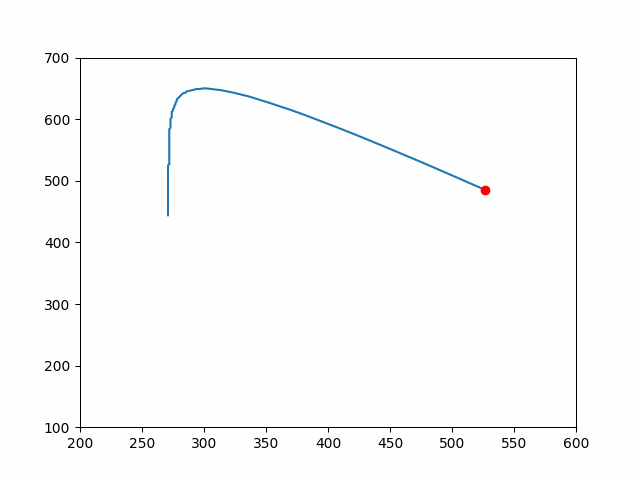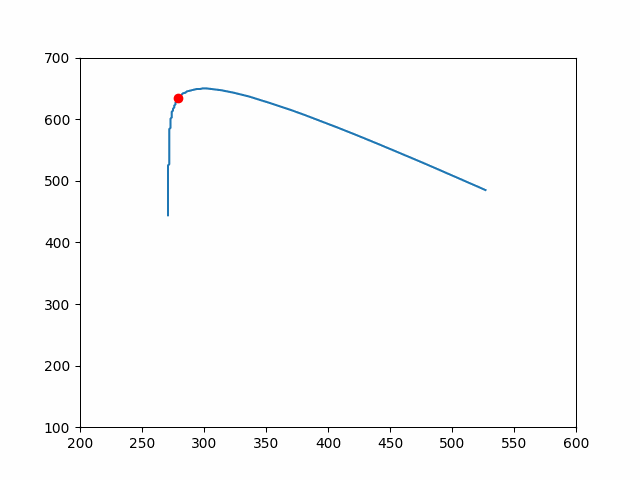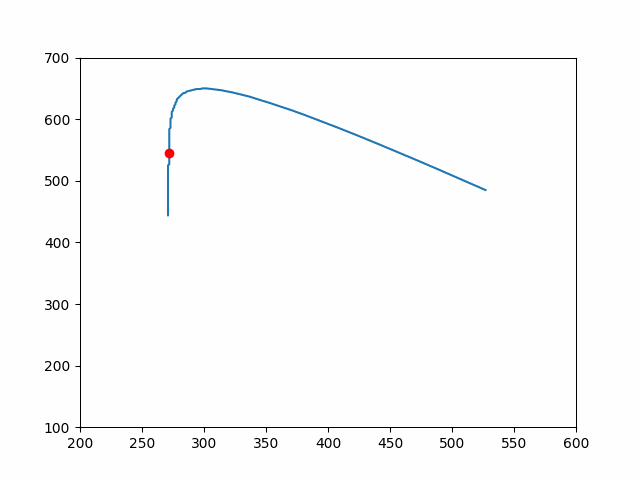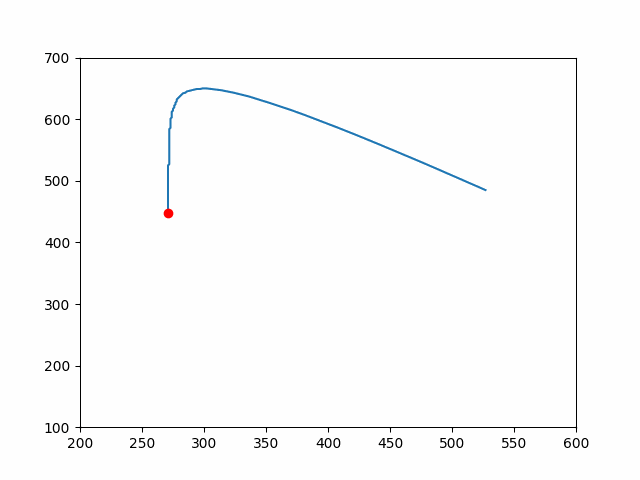
用一个边上为 10 的正方形，实现轨迹。

const fetti = {
  x: 445,
  y: 541,
  angle2D: (3 / 2) * Math.PI + (1 / 6) * Math.PI,
  color: { r: 20, g: 30, b: 50 },
  tick: 0,
  totalTicks: 200,
  decay: 0.9,
  gravity: 3,
  velocity: 50,
};
var animationFrame = null;
const update = () => {
  context.clearRect(0, 0, canvas.width, canvas.height);
  context.fillStyle = "rgba(2, 255, 255, 1)";
  context.beginPath();
  fetti.x += Math.cos(fetti.angle2D) * fetti.velocity; // 第一个点
  fetti.y += Math.sin(fetti.angle2D) * fetti.velocity + fetti.gravity; // 第一个点

  var x1 = fetti.x;
  var y1 = fetti.y;

  var x2 = fetti.x; // 第二个点
  var y2 = fetti.y + 10; // 第二个点

  var x3 = x1 + 10;
  var y3 = y1 + 10;

  var x4 = fetti.x + 10;
  var y4 = fetti.y;

  fetti.velocity *= fetti.decay;

  context.moveTo(Math.floor(x1), Math.floor(y1));
  context.lineTo(Math.floor(x2), Math.floor(y2));
  context.lineTo(Math.floor(x3), Math.floor(y3));
  context.lineTo(Math.floor(x4), Math.floor(y4));

  context.closePath();
  context.fill();
  animationFrame = raf.frame(update);
};

是不是除了颜色和形状，有那味了？

# 反转特效

那么如何实现让这个下落更加自然，会有一种飘落的感觉呢？

其实，他就是一直在做一个翻转特效.

将他们拆解就是在做绕着一个点的旋转运动，整个过程就是一边自我翻转一边按照运动轨迹进行移动。

实现这个特效，其实之前在实现正方形的时候提到过，实现一个正方形。满足以下三个点能实现一个平行四边形。

知道一个点的位置
知道一个角度
知道一边边长

目前我能确定的有，一个点的位置很容易确定，就是我们的起始点，然后我们边长也知道，就差一个角度了，只要我们的角度不断变化，我们就能实现以上特效。

const update = () => {
  context.clearRect(0, 0, canvas.width, canvas.height);
  context.fillStyle = "rgba(2, 255, 255, 1)";
  context.beginPath();

  fetti.velocity *= fetti.decay;
  fetti.tiltAngle += 0.1; // 不断给这个四边形变化角度

  var length = 10;

  var x1 = fetti.x;
  var y1 = fetti.y;

  var x2 = fetti.x + length * Math.sin(fetti.tiltAngle); // 第二个点
  var y2 = fetti.y + length * Math.cos(fetti.tiltAngle); // 第二个点

  var x3 = x2 + 10;
  var y3 = y2;

  var x4 = fetti.x + length;
  var y4 = fetti.y;

  context.moveTo(Math.floor(x1), Math.floor(y1));
  context.lineTo(Math.floor(x2), Math.floor(y2));
  context.lineTo(Math.floor(x3), Math.floor(y3));
  context.lineTo(Math.floor(x4), Math.floor(y4));

  context.closePath();
  context.fill();
  animationFrame = raf.frame(update);
};

这样我们就实现了以上的特效。

# 组合运动

然后把我们以上写的组合在一起就是一个完整的特效啦。

const update = () => {
  context.clearRect(0, 0, canvas.width, canvas.height);
  context.fillStyle = "rgba(2, 255, 255, 1)";
  context.beginPath();
  fetti.x += Math.cos(fetti.angle2D) * fetti.velocity; // 第一个点
  fetti.y += Math.sin(fetti.angle2D) * fetti.velocity + fetti.gravity; // 第一个点

  fetti.velocity *= fetti.decay;
  fetti.tiltAngle += 0.1; // 不断给这个四边形变化角度

  var length = 10;

  var x1 = fetti.x;
  var y1 = fetti.y;

  var x2 = fetti.x + length * Math.sin(fetti.tiltAngle); // 第二个点
  var y2 = fetti.y + length * Math.cos(fetti.tiltAngle); // 第二个点

  var x3 = x2 + 10;
  var y3 = y2;

  var x4 = fetti.x + length;
  var y4 = fetti.y;

  context.moveTo(Math.floor(x1), Math.floor(y1));
  context.lineTo(Math.floor(x2), Math.floor(y2));
  context.lineTo(Math.floor(x3), Math.floor(y3));
  context.lineTo(Math.floor(x4), Math.floor(y4));

  context.closePath();
  context.fill();
  animationFrame = raf.frame(update);
};

# 最终形态

如果想要实现最后的状态，就差多个小块、渐变消失以及随机颜色了！

设置多少帧消失，这里搞了两个变量totalTicks和tick，自定义来控制多少帧后小块消失。

至于多个小块，我们只需要搞一个 for 循环。

而随机颜色，搞了一个colors列表。

const colors = [
  "#26ccff",
  "#a25afd",
  "#ff5e7e",
  "#88ff5a",
  "#fcff42",
  "#ffa62d",
  "#ff36ff",
];
var arr = [];
for (let i = 0; i < 20; i++) {
  arr.push({
    x: 445,
    y: 541,
    velocity: 45 * 0.5 + Math.random() * 20,
    angle2D: (3 / 2) * Math.PI + ((Math.random() * 1) / 4) * Math.PI,
    tiltAngle: Math.random() * Math.PI,
    color: hexToRgb(colors[Math.floor(Math.random() * 7)]),
    shape: "square",
    tick: 0,
    totalTicks: 200,
    decay: 0.9,
    random: 0,
    tiltSin: 0,
    tiltCos: 0,
    gravity: 3,
  });
}

完整代码请看

https://github.com/hua1995116/node-demo/blob/master/confetti/%E5%AE%8C%E6%95%B4demo.html

# 加点餐

实现多人对战形态的表情大战。在我们微信中表情的发送并不是单点的，而是多人形态，因此我们可以继续探索，利用 websocket 和多彩小块结合。

这里我们需要注意几个点。（由于篇幅原因就不对 websocket 展开讲解了，提一下实现要点）。

我们可以通过一个tag 来区分是历史消息还是实时消息
区分是自己发出的消息，还是受到别人的消息，来改变五彩纸屑方向。
只有为单个 🎉 的时候才会进行动画。
先进行放大缩小的动画，延迟 200ms 再出来特效

if (this.msg === "🎉" && this.status) {
  this.confetti = true;
  const rect = this.$refs.msg
    .querySelector(".msg-text")
    .getBoundingClientRect();
  if (rect.left && rect.top) {
    setTimeout(() => {
      confetti({
        particleCount: r(100, 150),
        angle: this.isSelf ? 120 : 60,
        spread: r(45, 80),
        origin: {
          x: rect.left / window.innerWidth,
          y: rect.top / window.innerHeight,
        },
      });
    }, 200);
  }
}

# 更多探索

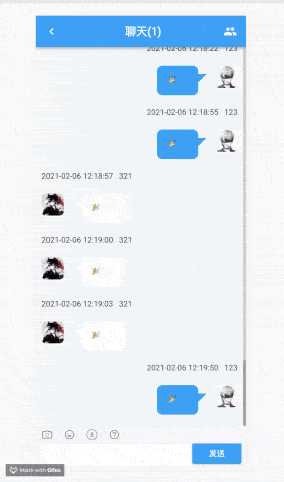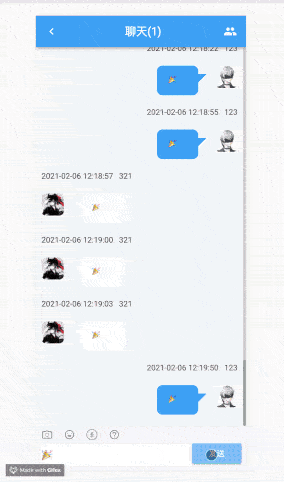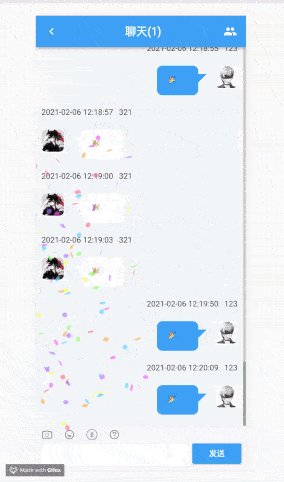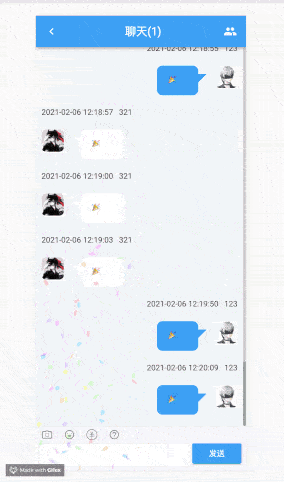
用 canvas 绘制非常非常多方块的时候，会比较卡顿，这个时候我们可以利用 web worker 来进行计算，从而提高性能，这个就请读者们自行探索啦，也可以看 canvas-confetti的源码~

# 最后

回看笔者往期高赞文章，也许能收获更多喔！

从破解某设计网站谈前端水印(详细教程) (opens new window)：790+点赞量
从王者荣耀里我学会的前端新手指引 (opens new window)：260+点赞量
一文带你层层解锁「文件下载」的奥秘 (opens new window)：140+点赞量
10 种跨域解决方案（附终极大招） (opens new window)：940+点赞量
一文了解文件上传全过程（1.8w 字深度解析，进阶必备） (opens new window)：260+点赞量

# 结语

❤️ 关注+点赞+收藏+评论+转发 ❤️，原创不易，鼓励笔者创作更好的文章

关注公众号秋风的笔记，一个专注于前端面试、工程化、开源的前端公众号

关注后回复简历获取 100+套的精美简历模板
关注后回复好友拉你进技术交流群+面试交流群
欢迎关注秋风的笔记